Simulation and Comparison Between Controls for Two-Wheeled Self-Balancing Robot

Analyzing PID and LQR Controllers in Matlab/simulink

Robot

Project Information

Project Overview

This project addresses the challenge of balancing an inverted pendulum using a two-wheeled self-balancing robot. It explores various control strategies, including PID and LQR, through MATLAB/Simulink simulations along with the feasibility with studying the motor current responses since aggressive control might resulting on damages of motor due to heat resulting from surge of current in coil.

Methodology

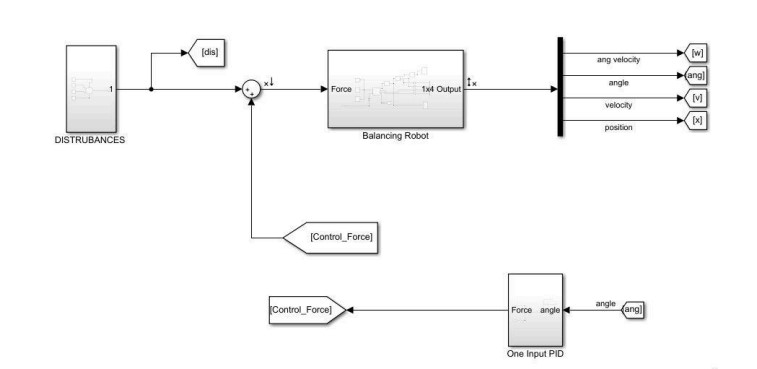
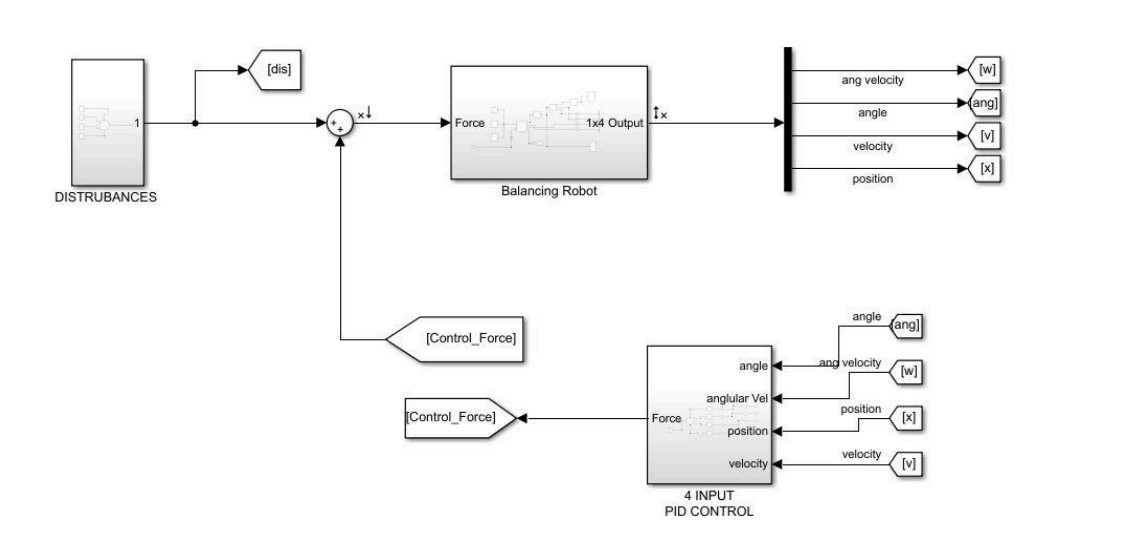
PID Response
PID Block Diagram
PID Response
Aggressive PID Block Diagram
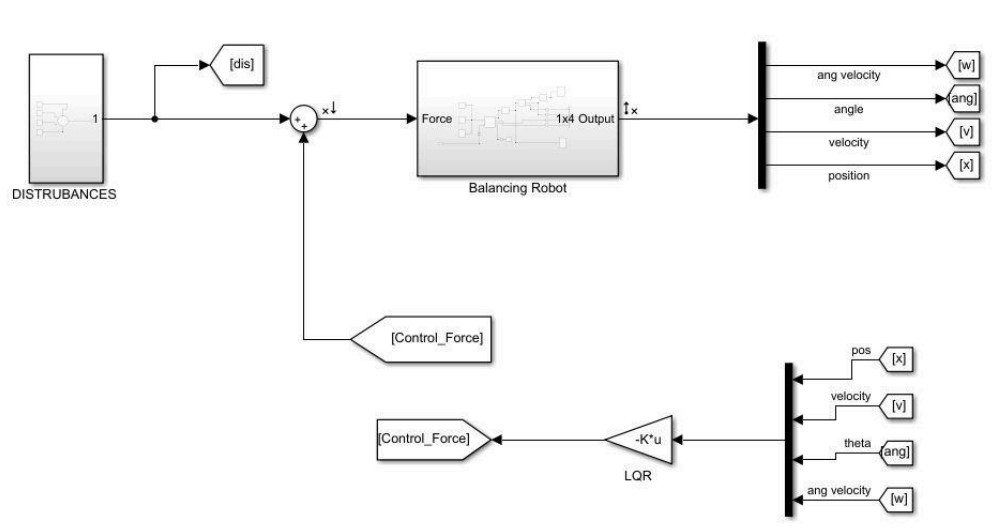
LQR Response
LQR Block Diagram
  • Mathematical Modeling: The mechanical system was modeled as an inverted pendulum on a cart, reducing degrees of freedom for analysis.
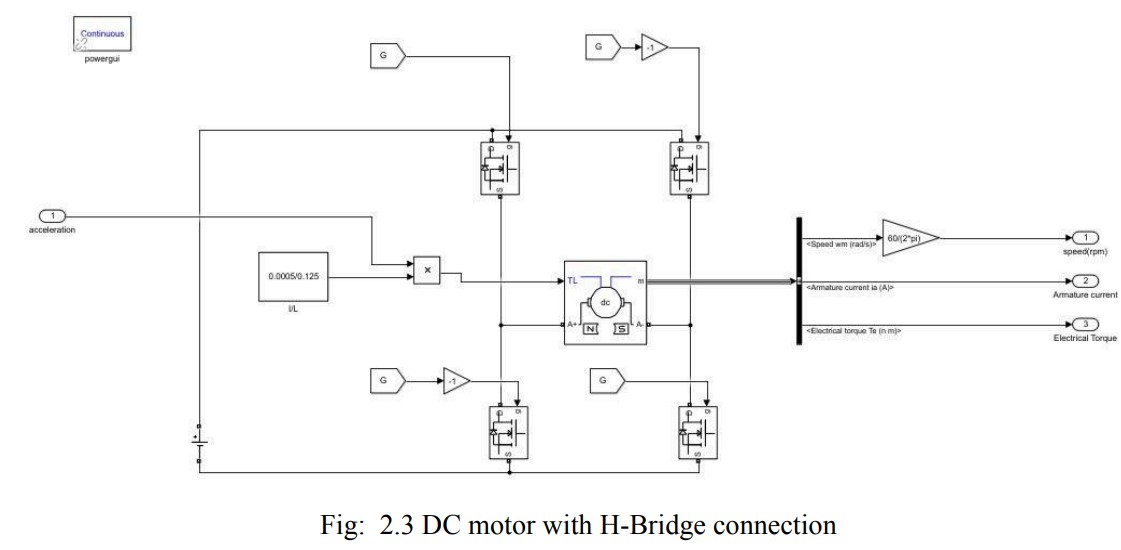
  • DC Motor Response: Modeled using characteristics like 6V input, 0.7Ω resistance, and back EMF (0.08 V/rpm). Current and speed responses were analyzed to ensure feasibility.
  • PID Controller: Single and multi-loop PID systems were tested. Multi-loop provided enhanced stability by integrating angular and linear velocity feedback.
  • LQR Control: An optimal controller was designed to minimize the system's cost function, balancing control effort with performance accuracy.
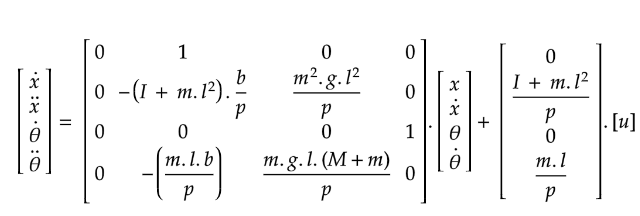
    • PID Response
    State representation of robot
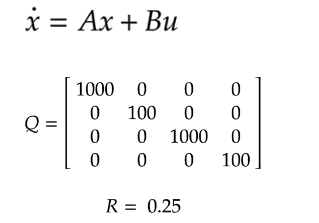
    LQR Response
    Tuned values for LQR

    Motor Analysis

    Motor Specifications:

    • Input Voltage: 6V
    • Armature Resistance: 0.7Ω
    • Back EMF Constant: 0.08 V/rpm

    The motor's response was critical in assessing the feasibility of different control strategies. Current and speed characteristics were observed under various disturbances.

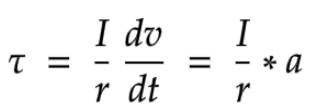
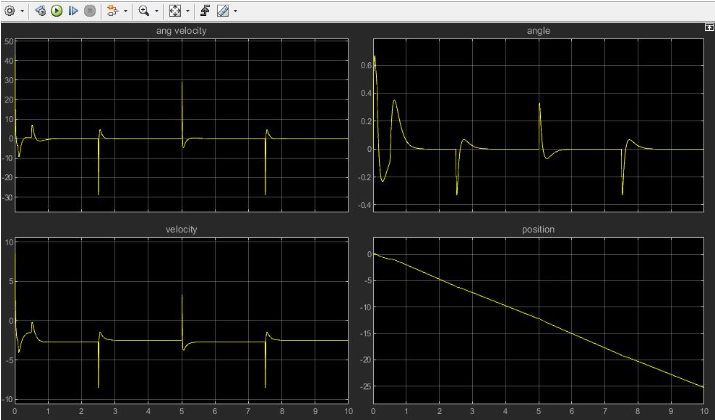
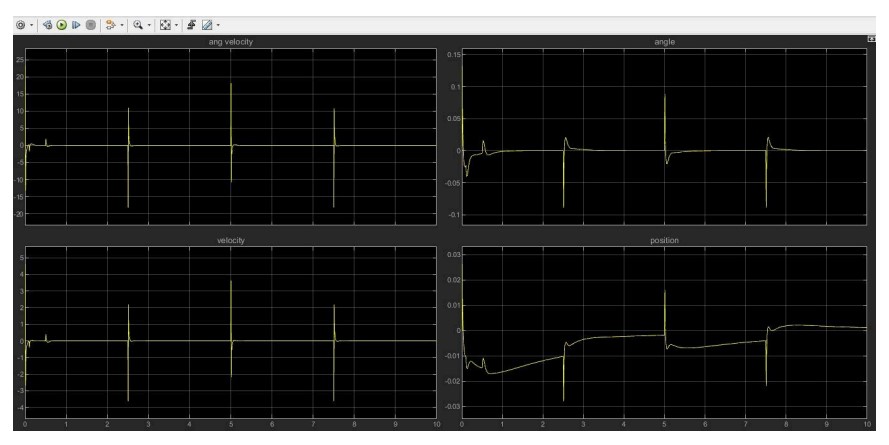
    PID Response
    Relation between Torque(o/p) to Current
    PID Response
    Driving motor accordance to gate pulse as well as the relations
    PID Response
    PID Controller Response
    PID Response
    Agressive PID Controller Response
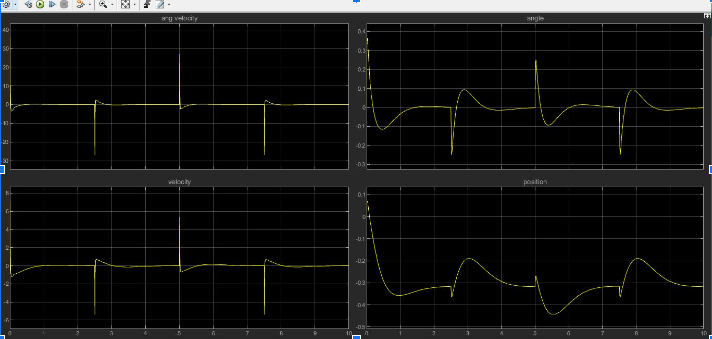
    LQR Response
    LQR Controller Response
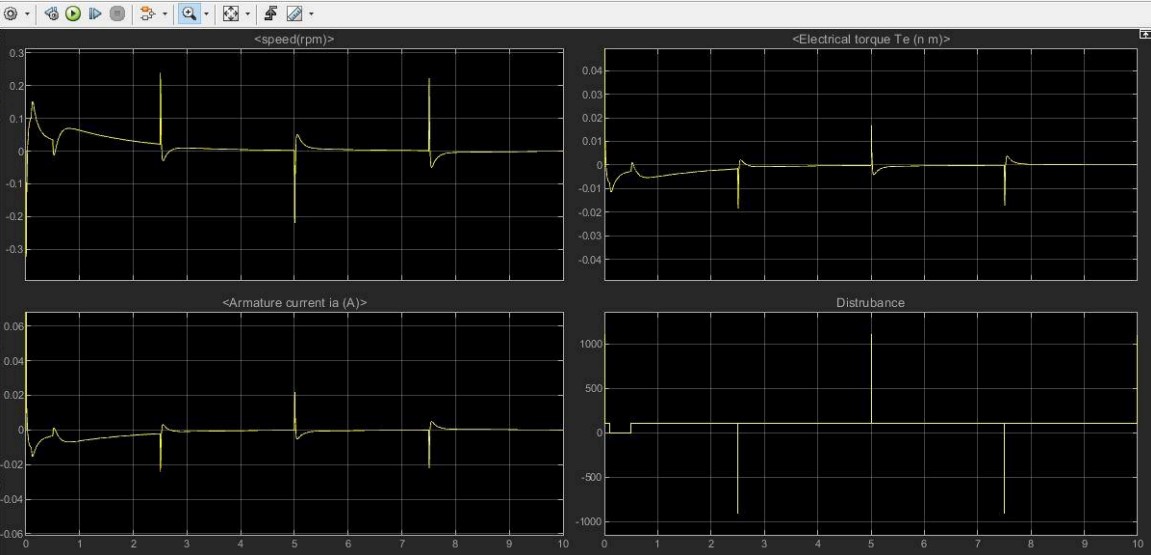
    Motor Response with PID Controller
    Motor Response with Single PID Controller
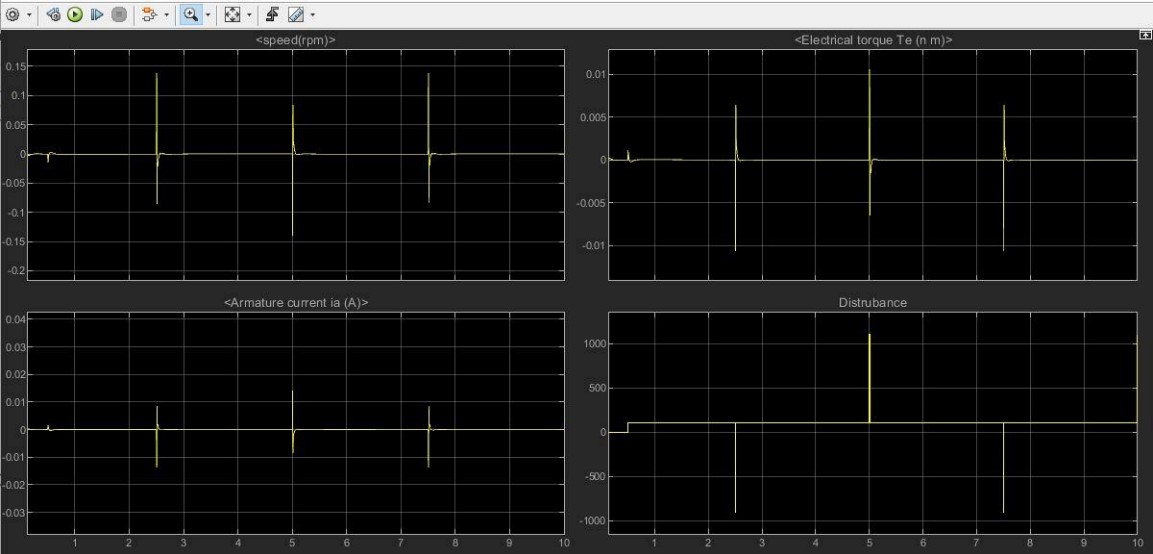
    PID Response
    Agressive PID Motor Response
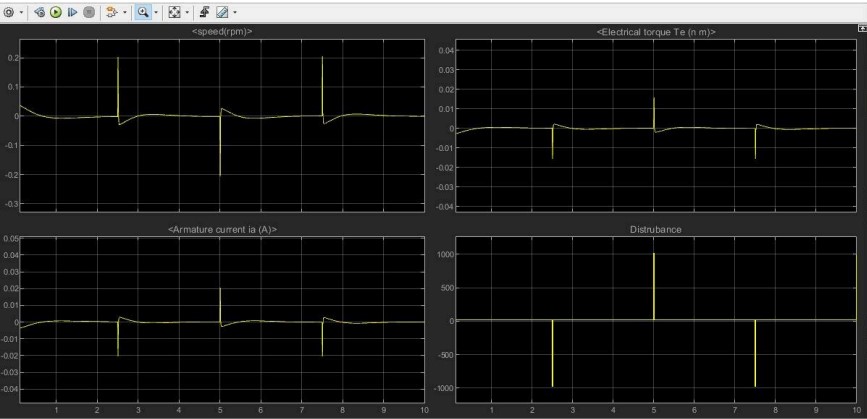
    Motor Response with LQR Controller
    Motor Response with LQR Controller

    Results

    PID Controllers: PID stabilized the robot but resulted in continuous motion to compensate for disturbances. Contrastingly, Agressive pid capable of stabilizing the position in closed confinement, however suffers from high transient motor current which might be fatal.

    LQR Controller: Achieved superior performance with lower energy consumption and smoother motor response. Current spikes were reduced, and the system remained stable under varying disturbances.

    Conclusion

    The LQR controller demonstrated optimal performance, balancing the robot efficiently with minimal energy usage. Future work includes real-world validation and noise reduction for enhanced robustness.